Algoritma Nedir? Algoritma Örnekleri ve Algoritma Analizi

Algoritma bir problemi çözmek adına sırayla tanımlanmış adımlar dizisidir. Başka bir şekilde ifade edersek kısaca çözüm diyebiliriz. Genellikle bilgisayarla özdeşleştirilen algoritmalar günlük hayatımızda her yerde karşımıza çıkabilir. Yemek tarifi, bir evin düzen planlanması, bir öğrencinin ödevini yapması gibi içinde çözülmesi gereken bir eylem barındırması yeterlidir.
Peki bir algoritmayı iyi yapan özellikleri var mıdır?
Her adımın açık ve net olması gerekir. Girdi ve çıktılar tam olarak tanımlanmalıdır. Algoritmalar bilgisayar kodu ile karıştırılmamalıdır. Algoritma bilgisayar kodu içermez, içermemelidir.
Peki bilgisayar programları, programlama dilleri neden algoritma kullanmaktadır?
Bilgisayarların ilk kullanım alanlarına bakarsak çözülmesi zor ya da yıllar sürecek matematik problemlerini çözmek amaçlı çıktığını fark etmekteyiz. Ortada bir problem var ve de bilgisayarı bu problemi çözmek doğrultusunda kullanıyoruz. Yapısı gereği bir bilgisayar net girdiler ister. Sezgilerle değil, kesin ve açık adımlarla çalışır. Bu nedenle algoritmalar bilgisayar biliminde kullanılmaktadır.
Algoritma Örnekleri
Kullanıcı tarafından girilen iki sayının toplamını veren bir algoritma örneği:
ilk adım: Birinci sayıyı, ikinci sayıyı ve toplamı tanımla.
ikinci adım: Kullanıcıdan sayıları girmesini iste.
üçüncü adım: Kullanıcının girdiği sayıları oku.
dördüncü adım: İki sayıyı topla.
beşinci adım: Sayıyı sonuca ata.
altıncı adım: Sonucu yansıt. Gördüğünüz gibi yazdığımız algoritmada herhangi bir bilgisayar kodu görmemekteyiz. Bununla birlikte her adım net ve anlaşılır bir şekilde ifade edilmiştir.
Kullanıcı tarafından girilen üç sayı arasında en büyük olanını bulan bir algoritma örneği:
1. adım: a, b, c adında değişkenler tanımla.
2. adım: Kullanıcıdan sayıları girmesini iste.
3. adım: Kullanıcının girdiği sayıları oku.
4. adım: Değişkenlere sayıları ata.
5. adım:
5.1 adım: Eğer a sayısı b sayısından büyükse; a sayısı c sayısından büyük mü diye bak.
5.1.1 adım: Eğer a sayısı c sayısından büyükse a sayısını sonuç olarak göster.
5.1.2 adım: Eğer a sayısı c sayısından büyük değilse c sayısını sonuç olarak göster.
5.2 adım: Eğer a sayısı b sayısından büyük değilse; b sayısı c sayısından büyük mü diye bak.
5.2.1 adım: Eğer b sayısı c sayısından büyükse b sayısını sonuç olarak göster.
5.2.2 adım: Eğer b sayısı c sayısından büyük değilse c sayısını sonuç olarak göster.
Her ne kadar günlük hayatta kullanıldığından bahsetsek de özellikle bilgisayarda kullanıldığı konusunda hemfikiriz. Peki her algoritmayı bilgisayarlarda kullanabilir miyiz? Bunları birbirlerinden ayıran bir yanı var mıdır? Google’ın milyonlarca sayfayı saniyeler içerisinde getiren algoritmasını diğerlerinden ayıran ne?
Sorunun içinde cevabını verdik aslında, saniyeler içinde getirmesi. Başka kelimelerle hızlı olması. Bir algoritmanın performansı onun kullanılmasını belirleyecektir.
Algoritma Analizi: Asimptotik Analizi
Bir algoritmanın verimliliği, algoritmayı yürütmek için gereken süreye, depolamaya ve diğer kaynaklara bağlıdır. Algoritmanın verimliliği veri büyüklüğüne göre analiz edilir. Kısacası veri arttıkça geçen süre ve depolama alanı ölçülür.
Bir algoritmayı analiz ederken bilgisayarın o algoritmayı çalıştırması için gereken süre, harcaması gereken depolama alanına bakarız. Buna göre algoritmanın nasıl bir sonuç vereceğini hesaplarız.
Bunu bir örnekle açıklayalım.
Elimizde 100 rakam var. Biz bu rakamları sıralı bir şekilde, küçükten büyüğe yazdırmak istiyoruz. Eğer sayılar çoktan sıralanmış ise harcayacağımız zaman, sıralanmamış haline göre az olacaktır. Ya da bu sefer elimizde 1000 sayı olsun. Yine harcayacağımız depolama alanı ve zaman değişecektir. Bu gibi değişkenler doğrultusunda bir algoritmanın performansını analiz edebiliyoruz.
Ve bu konuda asimptotik notasyonlardan faydalanırız. Asimptotik notasyolar, girdi belirli bir değere veya sınırlayıcı bir değere yöneldiğinde bir algoritmanın çalışma süresini açıklamak için kullanılan matematiksel notasyonlardır.
Asimptotik Notasyonlar: Theta notasyonu, Omega notasyonu and Big-O notasyonu.
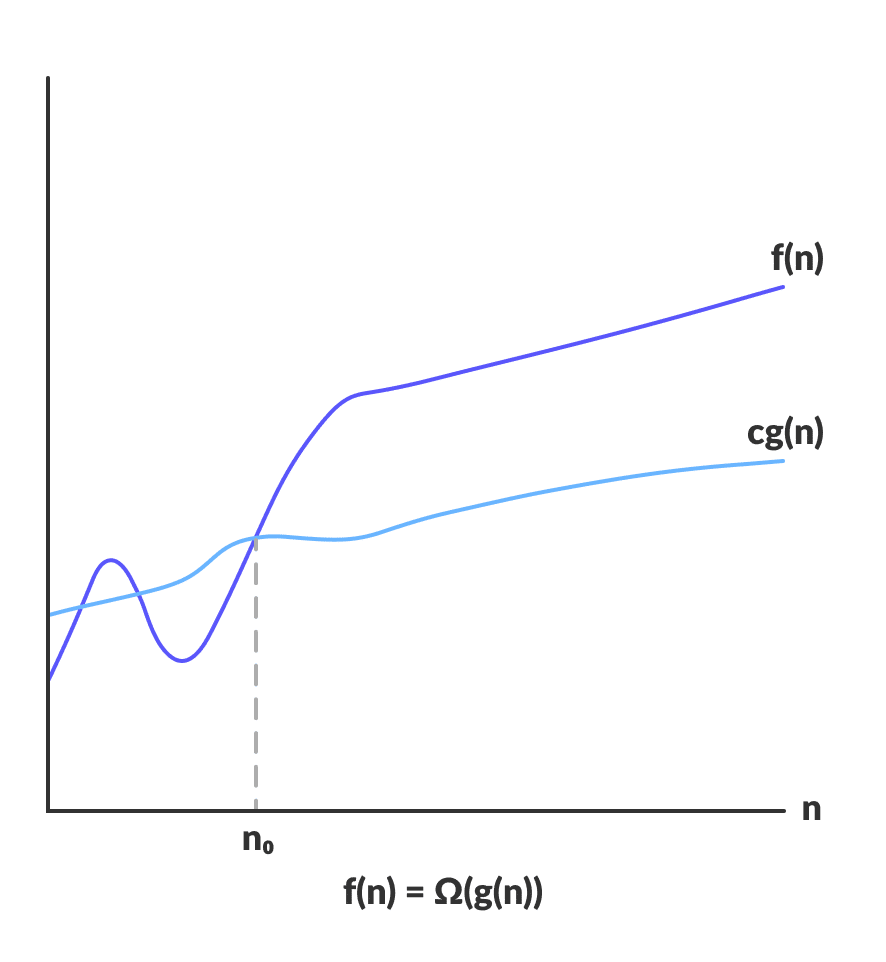
Theta Notasyonu (Θ – Notasyonu)
Theta notasyonu ile ölçtüğümüz bir algoritmanın ortalama alacağı süredir. Örnekteki algoritmaya bakarsak, birçok denemenin ardından bir grafiğe yansıtıldığını görürüz.
C2g(n) değeri algoritmanın çalışması için gerekli sürenin maksimum olduğu süredir.
Öte yandan C1gn(n) değeri algoritmanın çalışması gerekli sürenin minimum olduğu süredir.
Bu doğrultuda f(n) yani theta notasyonu, ortalama geçen süreyi bize vermektedir.
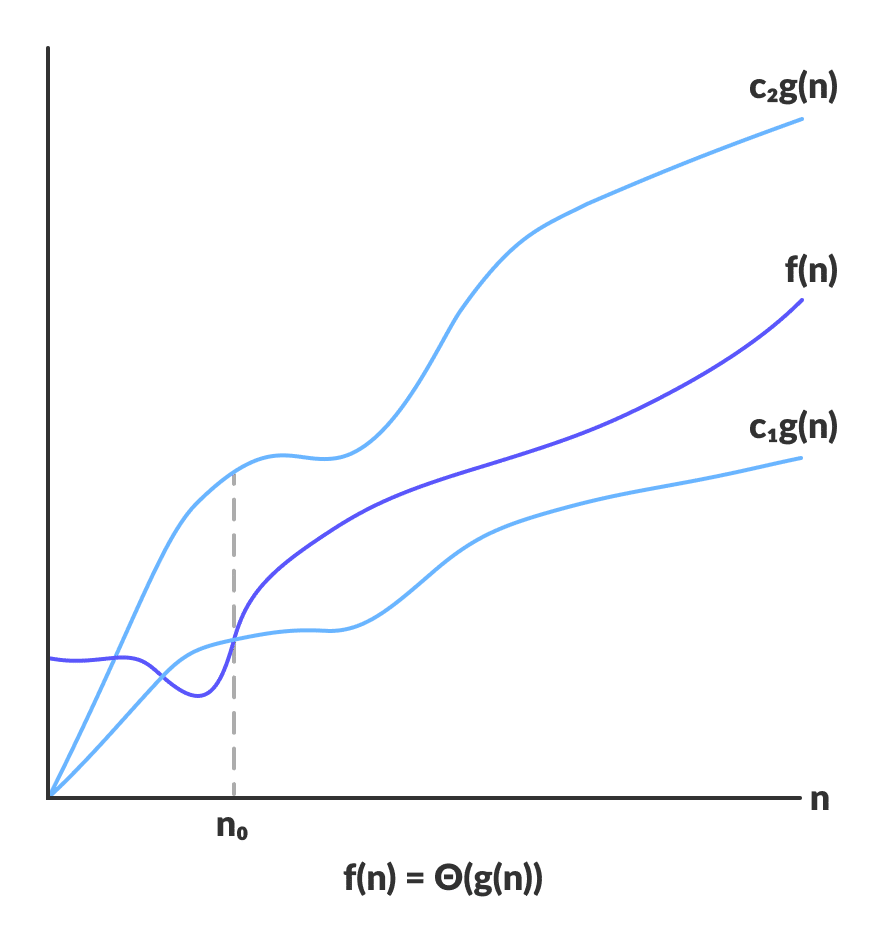
Büyük-O Notasyonu (O – Notasyonu)
Büyük O notasyonu bir algoritma için harcanan sürenin maksimum halini baz alır. Bir başka şekilde algoritmanın en kötü çalışma şeklini hesaplar.
Çoğu zaman bilgisayar programlarında baz alınan büyük o notasyonu olmaktadır. Bunun birincil nedeni bir algoritmanın vereceği en kötü sonucu bilinirse, harcanması gereken süre ve de depolama alanı öngörülebilir.
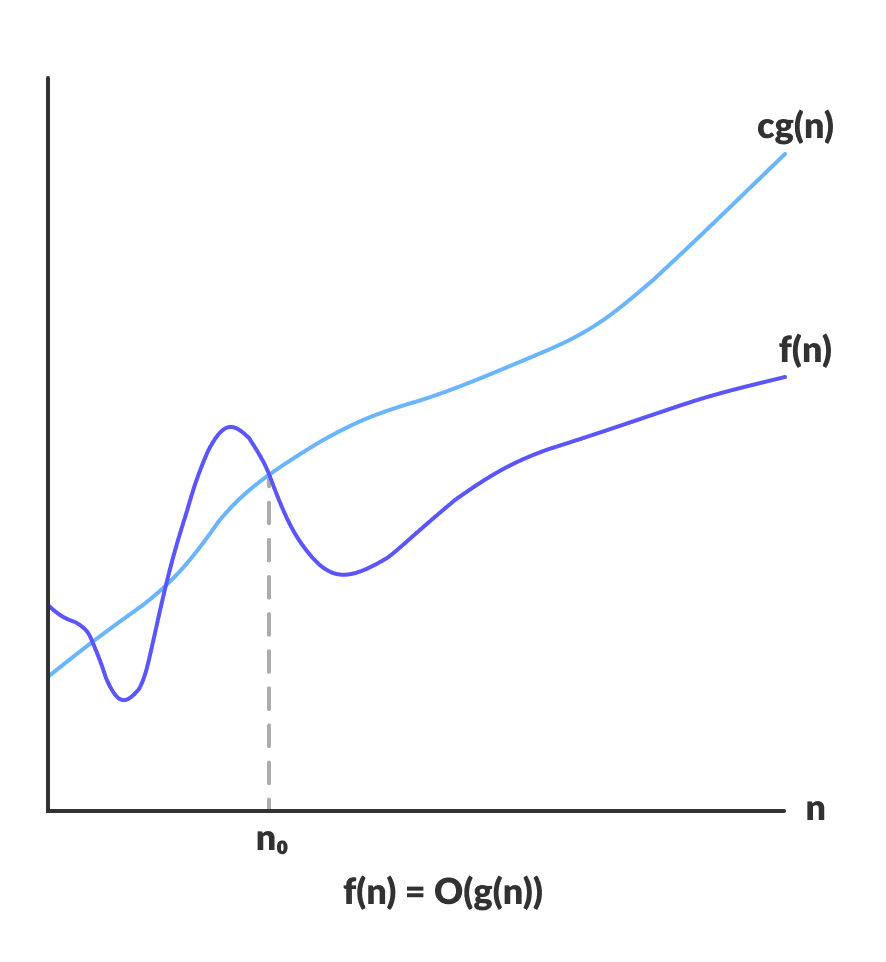
Omega Notasyonu (Ω – Notasyonu)
Omega notasyonu bir algoritma için harcanan sürenin minimum halini baz alır. Bir başka şekilde algoritmanın en iyi çalışma şeklini hesaplar.
Kısaca bahsettiklerimizi toparlamamız gerekirse,
Algoritma bir problem doğrultusunda izlenmesi gereken kurallı, sıralı ve açık adımlardan oluşan bir dizi bütünüdür. Algoritmalar günlük hayatta olmak üzere birçok alanda karşımıza çıkmaktadır. Özellikle bilgisayar biliminde görmekteyiz. Her algoritma aynı sonucu vermez, performans farkları vardır. Bu doğrultuda algoritmaların performansları, verimlilikleri ölçülür.
En yaygın bilinen verimlilik analizi; asimptotik analizidir. Asimptotik Analiz algoritma için geçen süreyi ve depolama alanını girdinin büyümesine bağlı olarak ölçer.
En çok bilinen üç asimptotik notasyonları: Theta, Büyük O ve de Omega Notasyonlarıdır. Aralarında bilgisayar biliminde en çok kullanılan notasyon, Büyük O notasyonudur.